You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What are the possible formations of just the dimension of time in a Minkowski space?
- Thread starter Mates
- Start date
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
If you are looking at just the time component it would simply be a line (or some kind of curve depending on the motion of the rock.) Otherwise the worldsheet is a surface in a 5D space.For example, what shape of worldline would a rock in an inertial frame have? Or is this impossible to know?
-Dan
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
The world sheet describes the whole of space-time in one fell swoop. Think of it this way... if we want to look at the whole of the motion of an object in 2D it is more convenient to look "down" at it from a 3D perspective. Then we can see the whole thing at once.
-Dan
-Dan
Ok that makes sense.The world sheet describes the whole of space-time in one fell swoop. Think of it this way... if we want to look at the whole of the motion of an object in 2D it is more convenient to look "down" at it from a 3D perspective. Then we can see the whole thing at once.
-Dan
I am having a small issue with how the Minkowski distance formula works. It is ds^2 = -c^2dt^2 + dx^2 + dy^2 +dz^2, but if I set dy and dz to 0 meters and just plug in dx = 1 meter and dt = 1 second, I get the square root of 1 - c, a large negative number. What am I doing wrong?
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Nothing. The Minkowski "distance formula" is not really a distance formula. It is not an inner product as it has what's called an indefinite norm (meaning that [imath]ds^2[/imath] can become negative) so we can't really call it a distance. It does have the useful property of being invariant under a Lorentz transformation. Note that if we set dt = 0 then ds does become a real number.Ok that makes sense.
I am having a small issue with how the Minkowski distance formula works. It is ds^2 = -c^2dt^2 + dx^2 + dy^2 +dz^2, but if I set dy and dz to 0 meters and just plug in dx = 1 meter and dt = 1 second, I get the square root of 1 - c, a large negative number. What am I doing wrong?
-Dan
Addendum: Usually in SR we set the unit system so that c = 1 (unitless.) So the units for distance and time are the same, conventionally called distance, and this "normalizes" the system so that the numbers work out to be a bit nicer. In fact, in your case [imath]ds^2 = 1 - c = 1 - 1 = 0[/imath], which is a real number and would have lead you to the wrong conclusion about the "distance formula!"
-Dan
It is perplexing to think of how two parallel worldlines work in general relativity.Nothing. The Minkowski "distance formula" is not really a distance formula. It is not an inner product as it has what's called an indefinite norm (meaning that [imath]ds^2[/imath] can become negative) so we can't really call it a distance. It does have the useful property of being invariant under a Lorentz transformation. Note that if we set dt = 0 then ds does become a real number.
-Dan
Addendum: Usually in SR we set the unit system so that c = 1 (unitless.) So the units for distance and time are the same, conventionally called distance, and this "normalizes" the system so that the numbers work out to be a bit nicer. In fact, in your case [imath]ds^2 = 1 - c = 1 - 1 = 0[/imath], which is a real number and would have lead you to the wrong conclusion about the "distance formula!"
-Dan
I am imagining 2 rocks at rest with each other on a time over distance graph. Their worldlines would be two parallel lines running vertically. At any instant, we can say that the rocks are a real distance d apart. So we can imagine that the parallel worlines exist exactly as they would appear on a t over distance graph.
But the Minkowski metric does not agree with the parallel line image when any dt is not equal to zero. So doesn't this seem like a contradiction?
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Remember the distance is not given by [imath]ds^2[/imath]. [imath]ds^2[/imath] is called the "interval." The distance formula is still the same as it is in the Pythagorean theorem. I know I alluded to this in an above post, and I'm sorry for the confusion!It is perplexing to think of how two parallel worldlines work in general relativity.
I am imagining 2 rocks at rest with each other on a time over distance graph. Their worldlines would be two parallel lines running vertically. At any instant, we can say that the rocks are a real distance d apart. So we can imagine that the parallel worlines exist exactly as they would appear on a t over distance graph.
But the Minkowski metric does not agree with the parallel line image when any dt is not equal to zero. So doesn't this seem like a contradiction?
-Dan
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Yes, they would be parallel lines. (However, not to muddy things, parallel and perpendicular are both defined differently for intervals. Using the 3D concept, ie. the Pythagorean theorem, then yes they are parallel.)So then would the parallel lines in my example exist in real life as they do in the graph in my example?
-Dan
If the rocks were 5 meters apart, would their worldlines exist 5 meters apart in real life? The reason why I am asking this is because I wonder what would happen if there was another point of view from a fast moving object relative to the rocks. In the diagram on the left, the red line is the worldline of the fast moving object from its frame of reference. The diagram on the right is the frame of reference of the two rocks. How would the worldlines actually exist?Yes, they would be parallel lines. (However, not to muddy things, parallel and perpendicular are both defined differently for intervals. Using the 3D concept, ie. the Pythagorean theorem, then yes they are parallel.)
-Dan
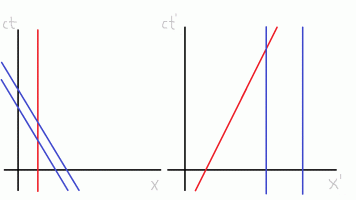
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Yes, the rocks would be 5 m apart at all times (so long as they aren't moving with respect to each other, of course!) If the observer moving at speed is moving at some velocity with a component parallel to the line connecting the rocks then they will observe the distance to be smaller than 5 m. This is length contraction (or the Fitzgerald contraction) effect.
-Dan
-Dan
This is the point where things become very confusing for me. I have always read that each observer is correct. For example, the two rocks may be 5m apart in their frame, the righthand diagram. But for the frame on the left side, for the, let's call it a bullet, the rocks may be 3m apart (I know that my worldline angles are probably wrong for this exact length contraction).
I assume that both diagrams of this simple block universe cannot exist because then there would be 4 rocks, 2 bullets, ect.
So I wonder what formation actually would exist. Could it be just the Minkowski metric? But that doesn't seem right either because the Minkowski metric turns into a Euclidean metric as we saw with the parallel lines.
I assume that both diagrams of this simple block universe cannot exist because then there would be 4 rocks, 2 bullets, ect.
So I wonder what formation actually would exist. Could it be just the Minkowski metric? But that doesn't seem right either because the Minkowski metric turns into a Euclidean metric as we saw with the parallel lines.
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
The Minkowski metric is correct. The Lorentz transformations depend on a factor [imath]\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}[/imath]. The larger the value of v the larger the value of [imath]\gamma[/imath]. Specifically [imath]L' = \dfrac{L}{\gamma}[/imath]. So for a traveler seeing the rocks as he moves he will have a [imath]\gamma[/imath] larger than 1 and will see a smaller distance between the two rocks. But an observer on the ground with the rocks and not moving will have a [imath]\gamma = 1[/imath] so will measure the value as in the Pythagorean theorem.
-Dan
-Dan
Yes, I agree that is correct.The Minkowski metric is correct. The Lorentz transformations depend on a factor [imath]\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}[/imath]. The larger the value of v the larger the value of [imath]\gamma[/imath]. Specifically [imath]L' = \dfrac{L}{\gamma}[/imath]. So for a traveler seeing the rocks as he moves he will have a [imath]\gamma[/imath] larger than 1 and will see a smaller distance between the two rocks. But an observer on the ground with the rocks and not moving will have a [imath]\gamma = 1[/imath] so will measure the value as in the Pythagorean theorem.
-Dan
I don't think I was very clear.
My concern is about which formation would actually exist. There seem to be 3 possible formations in my example; each diagram and the Minkowski diagram (that cannot be shown because of the nature of the Minkowski space).
I think that the actual/real formation would be the Minkowski space diagram. Do you agree?
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Yes.Yes, I agree that is correct.
I don't think I was very clear.
My concern is about which formation would actually exist. There seem to be 3 possible formations in my example; each diagram and the Minkowski diagram (that cannot be shown because of the nature of the Minkowski space).
I think that the actual/real formation would be the Minkowski space diagram. Do you agree?
-Dan
I am really interested to know what form or what properties the time dimension has. I have been told that it is not possible to view the time dimension as in the example above. But can't we at least say that the time dimension is straight since it is only 1 extra dimension that intersects with the space dimension?
But then if that is true, why can't we see it or at least imagine it?
But then if that is true, why can't we see it or at least imagine it?
topsquark
Senior Member
- Joined
- Aug 27, 2012
- Messages
- 2,370
Of course we can imagine it. We imagine it as a straight line! I see no reason why we can't do that.I am really interested to know what form or what properties the time dimension has. I have been told that it is not possible to view the time dimension as in the example above. But can't we at least say that the time dimension is straight since it is only 1 extra dimension that intersects with the space dimension?
But then if that is true, why can't we see it or at least imagine it?
However if we are going to match it up with spatial axes we do have a problem. Minkowski space-time involves what is known as an "indefinite metric" which (more or less) implies that the time axis counts off in imaginary numbers. I suspect that is why you are being told that you can't imagine it.
And if the speed of light were much smaller we would see the effects of the Minkowski metric so we'd have a much more intuitive grasp on how the time axis interplays with the spatial ones. It's not that we really can't imagine it, it's that we don't have much experience thinking about it.
At least, that's my take.
-Dan
So is it sort of like a straight line that projects in a direction that cannot be illustrated? Or is an imaginary dimension even weirder than that?Of course we can imagine it. We imagine it as a straight line! I see no reason why we can't do that.
However if we are going to match it up with spatial axes we do have a problem. Minkowski space-time involves what is known as an "indefinite metric" which (more or less) implies that the time axis counts off in imaginary numbers. I suspect that is why you are being told that you can't imagine it.
And if the speed of light were much smaller we would see the effects of the Minkowski metric so we'd have a much more intuitive grasp on how the time axis interplays with the spatial ones. It's not that we really can't imagine it, it's that we don't have much experience thinking about it.
At least, that's my take.
-Dan
