You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What does it mean (180⁰ - θ)?
- Thread starter Indranil
- Start date
- Joined
- Nov 24, 2012
- Messages
- 3,021
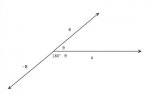
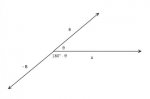
You said their sum, so how to add them like, sum = 180-θ + θ = 180⁰.Consider the following diagram:
View attachment 9755
The vectors \(\displaystyle \vec{B}\) and \(\displaystyle -\vec{B}\) simply form a line segment, and the angles \(\displaystyle \theta\) and \(\displaystyle 180^{\circ}-\theta\) are supplemental, meaning their sum is \(\displaystyle 180^{\circ}\).
- Joined
- Nov 24, 2012
- Messages
- 3,021
You said their sum, so how to add them like, sum = 180-θ + θ = 180⁰.
Yes, exactly.
mmm4444bot
Super Moderator
- Joined
- Oct 6, 2005
- Messages
- 10,962
It is the difference between two angle measurements (180° and θ).What does it mean (180⁰ - θ)?
Only when θ = 0°Does it mean 180⁰
180° = 1/2 revolution.
Example: You want 1/2 revolution. You rotate θ degrees, and that is less than 1/2 revolution. How much more rotation do you need?
The answer is 180° - θ
I have three questionsA and B vectors, the angle is θ, A and -B vectors, why the angle is 180⁰-θ? Could you simplify it, please?
1.'α' is what degree?
2.'β' is what degree?
3. What does '180⁰-θ' mean here? Please explain
Dr.Peterson
Elite Member
- Joined
- Nov 12, 2017
- Messages
- 16,855
I have three questions
1.'α' is what degree?
2.'β' is what degree?
3. What does '180⁰-θ' mean here? Please explain
I think lev888 meant that the angles are supplementary, meaning that their sum is 180°.
Angles alpha and beta are not relevant to your question; perhaps they are used later in the solution being shown. You can't calculate them knowing only theta.
All we know, given what you have shown, is that the sum α+β is equal to 180°-θ. That is because that angle is supplementary to the given angle θ, since vector A divides the straight angle formed by B and -B into two parts, which add up to a straight angle (180°).
One could say that 180°-θ means that we are taking angle θ away from that straight angle, and 180°-θ is what remains. That is, it is a subtraction.
In the future, please check whether your picture is clear before submitting. This is horribly fuzzy.