What is the measure of Angle A?
- Thread starter Gr8fu13
- Start date
burakaltr
Junior Member
- Joined
- Aug 26, 2011
- Messages
- 126
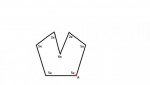
For the following polygon, what is the measure of angle A?
This is another one I am having a hard time starting. I see NOTHING in our reading materials that pertain to this
You can form 5 triangles inside the polygon which have angles' total equivalent to 180 (n-2)
And then proceed
Good Luck
So if 180(n-2)=total of all angles would it be:
180(7-2)=180 x 5 = 900 total for all angles?
When I broke each triangle down the measurements of the angles were 60 degrees so I would then take:
60 x 10 = 600 degrees
That leaves us with:
900 - 600 = 300 degrees.
Would that 300 degrees account for the top angle that is indented? It looks like it would be 300 degree
So the answer to the problem is that the angle of A would equal 120 degrees because I would add the two 60 degree angles from each triangle together. Right?
180(7-2)=180 x 5 = 900 total for all angles?
When I broke each triangle down the measurements of the angles were 60 degrees so I would then take:
60 x 10 = 600 degrees
That leaves us with:
900 - 600 = 300 degrees.
Would that 300 degrees account for the top angle that is indented? It looks like it would be 300 degree
So the answer to the problem is that the angle of A would equal 120 degrees because I would add the two 60 degree angles from each triangle together. Right?The "five triangles" approach is a good start.
The five triangles contain all the angles that are interior angles for the large polygon. Therefore the sum of the interior angles of the five triangles will be equal to the sum of the interior angles of the large polygon.
5(180) = 5x + 5x + 5x + 5x + 2x + 2x + 6x = 30x
x = 30
Angle A = 5x
The five triangles contain all the angles that are interior angles for the large polygon. Therefore the sum of the interior angles of the five triangles will be equal to the sum of the interior angles of the large polygon.
5(180) = 5x + 5x + 5x + 5x + 2x + 2x + 6x = 30x
x = 30
Angle A = 5x
So this is somewhat like a formula for figuring this out? So if it's that easy; then angle A would be 5 x 30 = 150 degrees. Right? I was not using the number in the polygon at all
Please do not think of this as "a formula for figuring it out." Draw the polygon, and draw the five triangles that can be made inside it. Study that figure until you can see logically and intuitively that the sum of the interior angles of the polygon are equal to the sum of the angles in the triangles. That is the type of insight you must develop to solve these kinds of problems -- not memorizing formulas.