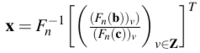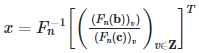Hello,
I would like to solve a linear equation
**Cx=b**
where **C** is a circulant square matrix with size n*x*n. By applying the circular convolution theorem, **discrete Fourier Transform** can be used to transform the cyclic convolution into component-wise multiplication written as
\(\displaystyle F_n(\textbf{c} \star \textbf{x}) = F_n(\textbf{c})F_n(\textbf{x}) = F_n(\textbf{b}) \)
so that
\(\displaystyle x = F_n^{-1}\bigg[\bigg( \frac{(F_n(\textbf{b}))_v)}{(F_n(\textbf{c}))_v}\bigg)_{v\in\textbf{Z}}\bigg]^T\) .
My question is how many number of FLOPs needed to calculate a vector **x**?
I would like to solve a linear equation
**Cx=b**
where **C** is a circulant square matrix with size n*x*n. By applying the circular convolution theorem, **discrete Fourier Transform** can be used to transform the cyclic convolution into component-wise multiplication written as
\(\displaystyle F_n(\textbf{c} \star \textbf{x}) = F_n(\textbf{c})F_n(\textbf{x}) = F_n(\textbf{b}) \)
so that
\(\displaystyle x = F_n^{-1}\bigg[\bigg( \frac{(F_n(\textbf{b}))_v)}{(F_n(\textbf{c}))_v}\bigg)_{v\in\textbf{Z}}\bigg]^T\) .
My question is how many number of FLOPs needed to calculate a vector **x**?