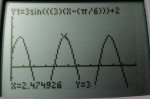
By two of the four solutions, do you mean the a, b, c, and d for problem 5a or possible there we 4 problems 5a), 5b), 5c), and 5d) and you got two of those correct? At a quick look it looks to me that you have three of the a, b, and, c correct for problem 5a). The a, b, and d. The c depends on whether you write the equation as a sine or as a cosine. Looking at the image of your paper I think I am seeing the two different formulas
\(\displaystyle 3\, sin[3\, (x\, -\, \frac{-\pi}{6})]\, +\, 2\)
and
\(\displaystyle 3\, cos[3\, (x\, -\, \frac{\pi}{3})]\, +\, 2\)
Those two equations are (almost) equivalent. I have to go right now but, if someone else doesn't chime in, I'll be back after a while when I get done with what I need to do.
O.K., back again. As I said, the c depends on whether you want to write the equation as a sine or a cosine. I find it easier to do the cosine first in general so I'll do that forst. The value of c is for x at the first maximum for x \(\displaystyle \ge\) 0 AND for the function going down. For this case, it is \(\displaystyle \frac{\pi}{3}\) so your function is
\(\displaystyle 3\, cos[3\, (x\, -\, \frac{\pi}{3})]\, +\, 2\)
That is one of the equations you have.
If you want to do the sine, you can do the cosine and add \(\displaystyle \frac{\pi}{2}\) to the argument or, look along the x=d line and find the first crossing for x \(\displaystyle \ge\) 0 AND for the function going up. In this case, it is \(\displaystyle \frac{\pi}{6}\) [looking at the image of the paper with the graph for problem 5a on it] so your function is
\(\displaystyle 3\, cos[3\, (x\, -\, \frac{\pi}{6})]\, +\, 2 = 3\, sin[3\, (x\, -\, \frac{\pi}{3}) + \frac{\pi}{2}]\, +\, 2\)
So you now see why I said the two answers were almost the same - change your \(\displaystyle \frac{-\pi}{6}\) where the function is going down to \(\displaystyle \frac{\pi}{6}\) where the function is going up and the answer would be correct.