logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,214
Of course. I know that you are here not to help me but I will give you some work because it is very rare to see a reply from you since the exposure of my identity.Are you going to show some work,
Here is my attempt. Okay, I assumed that it is not perpendicular, so what is the big deal of this assumption? I also provided a diagram of my assumption to show you how serious I am.Hint: Assume the line \(\displaystyle m\) is not perpendicular to the the segment \(\displaystyle \overline{QP}\).
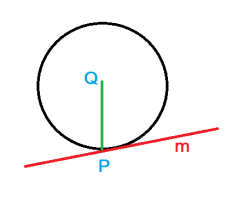
The discussion is now about the non-perpendicular assumption. When I prove it is perpendicular by contradiction, then I use this fact and the second assumption to prove it is tangent (this part should involve the secant).Non-tangent means secant, which means a proper triangle, which means no right angles.
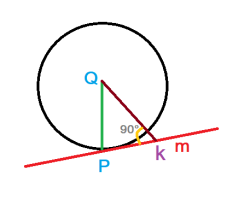
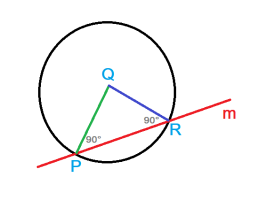
We need to assume thatProve the theorem by contradiction.
View attachment 39431
Hint: Assume the line \(\displaystyle m\) is not perpendicular to the the segment \(\displaystyle \overline{QP}\). Then assume the line \(\displaystyle m\) is not tangent to the circle.

Your statement here is like: Hey guys I am given line \(\displaystyle m\) that is tangent to the circle at point \(\displaystyle P\), but I will change its name to \(\displaystyle L\) and I will change the point \(\displaystyle P\) to \(\displaystyle T\). Then I will assume that this line is tangent to the circle. You are not assuming anything here because the line is already tangent to the circle. You are only changing its name and its point which will not affect anything.Define [imath]P[/imath]: "A line [imath]L[/imath] is tangent to a circle at point [imath]T[/imath]",
Tell me what exactly was not clear? I am not an expert like you in Geometry and Trigonometry but I can enlighten you as I have studied this proof for one month!The only issue I see is that your assumptions in each part of the proof are not entirely clear.
I am not against your idea here. It is perfectly fine. Only this should be changedThe only issue I see is that your assumptions in each part of the proof are not entirely clear. You are being asked to prove the following:
A line is tangent to a circle if and only if it is perpendicular to the radius at the point of intersection.
Define [imath]P[/imath]: "A line [imath]L[/imath] is tangent to a circle at point [imath]T[/imath]", and [imath]Q[/imath]: "The line [imath]L[/imath] is perpendicular to the radius at point [imath]T[/imath]".
We now want to prove [imath]P \Rightarrow Q[/imath]. That is, assume [imath]P[/imath] and [imath]\neg Q[/imath], and derive a contradiction.
In words: Assume there exists a line [imath]L[/imath] that is tangent to a circle at point [imath]T[/imath], but is not perpendicular to the radius through [imath]T[/imath].
For the converse direction, [imath]Q \Rightarrow P[/imath], suppose [imath]Q[/imath] and [imath]\neg P[/imath]; that is, assume the line [imath]L[/imath] is perpendicular to the radius at the point of intersection [imath]T[/imath], but that [imath]L[/imath] is not tangent to the circle. This assumption should lead to a contradiction.
Thanks for your reply — I see where you're coming from, but I don't fully agree.I am not against your idea here. It is perfectly fine. Only this should be changed
In words: You are given a line [imath]L[/imath] that is tangent to a circle at point [imath]T[/imath], but assume that it is not perpendicular to the radius through [imath]T[/imath].
You are given the line [imath]L[/imath] to be perpendicular to the radius at the point of intersection [imath]T[/imath], but assume that [imath]L[/imath] is not tangent to the circle.
The idea is that you cannot assume that the Earth has one Moon when it is a fact that it has one Moon. I hope that you understood my point.

I don't agree with saying we assume [imath]P[/imath] (that [imath]L[/imath] is tangent to the circle at [imath]T[/imath]). You should either say we are given this fact or you assume it is not tangent.Thanks for your reply — I see where you're coming from, but I don't fully agree.
According to your interpretation, we're given a line [imath]L[/imath] that is tangent to a circle at point [imath]T[/imath], and then we (incorrectly) assume that it is not perpendicular to the radius through [imath]T[/imath]. But in a proof by contradiction, we're not actually given such a line — we only suppose its existence for the sake of argument, in order to derive a contradiction.
In the case of [imath]P \Rightarrow Q[/imath], we assume [imath]P[/imath] (that [imath]L[/imath] is tangent to the circle at [imath]T[/imath]) and [imath]\neg Q[/imath] (that [imath]L[/imath] is not perpendicular to the radius at [imath]T[/imath]). From this, we deduce that [imath]L[/imath] must intersect the circle at another point — contradicting the assumption that [imath]L[/imath] is a tangent. That contradiction is what justifies [imath]P \Rightarrow Q[/imath].
So in this sense, the line isn't given as a real object with known properties — it's hypothetical, and its properties are assumed only temporarily to show that such a configuration cannot exist.
I've been reflecting on your reply and wanted to follow up with one more clarification.I don't agree with saying we assume [imath]P[/imath] (that [imath]L[/imath] is tangent to the circle at [imath]T[/imath]). You should either say we are given this fact or you assume it is not tangent.
As I said before you cannot assume something when it already does exist. Therefore, we are perfectly agreed that we totally don't agree to each other!
And thanks a lot for the rest of the idea!

Thank you a lot Aion for being so interested in one of my posts. This just reflects how much you love geometry particularly and proofs generally.I've been reflecting on your reply and wanted to follow up with one more clarification.
In my opinion, your reasoning is circular. You claim, “we don’t need to assume [imath]P[/imath] because [imath]P[/imath] is a fact.” But unless [imath]P[/imath] has been independently proven or specified as a given axiom, treating [imath]P[/imath] as a “fact” is itself an assumption. So you’ve effectively assumed [imath]P[/imath] in order to avoid assuming [imath]P[/imath], which is circular. This move resembles begging the question, because the point under debate—whether we are allowed to assume [imath]P[/imath]—is being taken for granted.In the Russian school facts cannot be assumed. So in my school you cannot assume \(\displaystyle P\) \(\displaystyle \left(\right.\)or \(\displaystyle P \rightarrow \lnot Q\)\(\displaystyle \left)\right.\), even if temporarily. We say that you will be given \(\displaystyle P\) and you will assume \(\displaystyle \lnot Q\). Here \(\displaystyle P\) and \(\displaystyle Q\) are facts!
In my opinion, your reasoning is circular. You claim, “we don’t need to assume [imath]P[/imath] because [imath]P[/imath] is a fact.” But unless [imath]P[/imath] has been independently proven or specified as a given axiom, treating [imath]P[/imath] as a “fact” is itself an assumption. So you’ve effectively assumed [imath]P[/imath] in order to avoid assuming [imath]P[/imath], which is circular. This move resembles begging the question, because the point under debate—whether we are allowed to assume [imath]P[/imath]—is being taken for granted.
