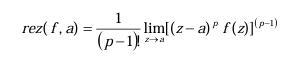You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Clueless about the Laplace Operational Method
- Thread starter wolly
- Start date
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
Yes.Can the pole be negative like -1 ?
Example of a negative pole:
\(\displaystyle F(s) = \frac{1}{(s + 1)^2}\)
\(\displaystyle s = -1\) is a negative pole of order \(\displaystyle 2\)
And 1 and 2 are poles of what order?Yes.
Example of a negative pole:
\(\displaystyle F(s) = \frac{1}{(s + 1)^2}\)
\(\displaystyle s = -1\) is a negative pole of order \(\displaystyle 2\)
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
A pole is a value that makes the denominator \(\displaystyle = 0\). A pole can have any order.And 1 and 2 are poles of what order?
For example:
\(\displaystyle F(s) = \frac{1}{(s - 1)} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 1\)
\(\displaystyle F(s) = \frac{1}{(s - 1)^2} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 2\)
\(\displaystyle F(s) = \frac{1}{(s - 1)^3} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 3\)
And
\(\displaystyle F(s) = \frac{1}{(s - 2)} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 1\)
\(\displaystyle F(s) = \frac{1}{(s - 2)^2} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 2\)
\(\displaystyle F(s) = \frac{1}{(s - 2)^{100}} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 100\)
Understood the idea?
How do you decide it's order?A pole is a value that makes the denominator \(\displaystyle = 0\). A pole can have any order.
For example:
\(\displaystyle F(s) = \frac{1}{(s - 1)} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 1\)
\(\displaystyle F(s) = \frac{1}{(s - 1)^2} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 2\)
\(\displaystyle F(s) = \frac{1}{(s - 1)^3} \rightarrow\) here \(\displaystyle s = 1\) is a pole of order \(\displaystyle 3\)
And
\(\displaystyle F(s) = \frac{1}{(s - 2)} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 1\)
\(\displaystyle F(s) = \frac{1}{(s - 2)^2} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 2\)
\(\displaystyle F(s) = \frac{1}{(s - 2)^{100}} \rightarrow\) here \(\displaystyle s = 2\) is a pole of order \(\displaystyle 100\)
Understood the idea?

logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
The power of the bracket.How do you decide it's order?
\(\displaystyle F(s) = \frac{1}{(s + 1)^p} \)
Here \(\displaystyle p\) is the order of the pole.
And i and -i?The power of the bracket.
\(\displaystyle F(s) = \frac{1}{(s + 1)^p} \)
Here \(\displaystyle p\) is the order of the pole.
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
Do you have an example of that in your mind? Or do you mean this:And i and -i?
\(\displaystyle F(s) = \frac{1}{(s + i)^p} \)
And this:
\(\displaystyle F(s) = \frac{1}{(s - i)^p} \)
??
For example If [math]z=2i[/math] and [math]z=-2i[/math]from the functionDo you have an example of that in your mind? Or do you mean this:
\(\displaystyle F(s) = \frac{1}{(s + i)^p} \)
And this:
\(\displaystyle F(s) = \frac{1}{(s - i)^p} \)
??
[math]f(z)=\frac{1}{z^2+4}[/math]
Which order would be 2i and -2i as a pole?
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
First factor the denominator.For example If [math]z=2i[/math] and [math]z=-2i[/math]from the function
[math]f(z)=\frac{1}{z^2+4}[/math]
Which order would be 2i and -2i as a pole?
\(\displaystyle f(z) = \frac{1}{z^2 + 4} = \frac{1}{(z + 2i)(z - 2i)}\)
So, we have two poles, \(\displaystyle z = 2i\) and \(\displaystyle z = -2i\), each one of them is of order one.
You always start by factoring first.Or
[math]\frac{10}{(z^2+4)(z^3-2z^2-z+2)} + \frac{z^2-z-4}{z^3-2z^2-z+2}[/math]
\(\displaystyle f(z) = \frac{10}{(z^2+4)(z^3-2z^2-z+2)} + \frac{z^2-z-4}{z^3-2z^2-z+2}\)
\(\displaystyle = \frac{10}{(z + 2i)(z - 2i)(z + 1)(z - 1)(z - 2)} + \frac{z^2-z-4}{(z + 2i)(z - 2i)(z + 1)(z - 1)(z - 2)}\)
Since the numerator \(\displaystyle z^2-z-4\) does not have a nice factor, it will not be cancelled with the denominator, so you leave it alone.
Now we collect the poles. These are the poles:
\(\displaystyle z = 2i\)
\(\displaystyle z = -2i\)
\(\displaystyle z = 1\)
\(\displaystyle z = -1\)
\(\displaystyle z = 2\)
Each one of them is of order one.
Last edited:
I have used the residue theorem but this is in a Laplace Operational method with
[math]Θ(p)=Y(p)*e^{pt}[/math]
Can p be irrational?If yes then how can it be solved in this equation?
@logistic_guy ?
It's based on the 2 functions which I wrote today.
[math]Θ(p)=Y(p)*e^{pt}[/math]
Can p be irrational?If yes then how can it be solved in this equation?
@logistic_guy ?
It's based on the 2 functions which I wrote today.
logistic_guy
Senior Member
- Joined
- Apr 17, 2024
- Messages
- 2,223
Yes it can be.Can p be irrational?If yes then how can it be solved in this equation?
The two functions that you wrote had real and imaginary poles, not irrational.It's based on the 2 functions which I wrote today.
An irrational pole will be something likes this:
\(\displaystyle f(z) = \frac{1}{z - \sqrt{2}}\)
Here \(\displaystyle z = \sqrt{2}\) is an irrational pole.
You can use the Laplace transform table.how can it be solved in this equation?
Or use the residue theorem.
So z tends to [math]-2i[/math] and [math]2i[/math]?Yes it can be.
The two functions that you wrote had real and imaginary poles, not irrational.
An irrational pole will be something likes this:
\(\displaystyle f(z) = \frac{1}{z - \sqrt{2}}\)
Here \(\displaystyle z = \sqrt{2}\) is an irrational pole.
You can use the Laplace transform table.
Or use the residue theorem.
[math]lim_{z \to 2i} f(z)*(z-2i)*e^{pt}[/math]and
[math]lim_{z \to -2i} f(z)*(z+2i)*e^{pt}[/math]
I mean I don't know how to calculate [math]e^{2it}[/math] and [math]e^{-2it}[/math]!
@logistic_guy
How does the denominator have these values?
[math]0![/math][math]1![/math][math]2![/math]@logistic_guy
Can you please explain?
[math]0![/math][math]1![/math][math]2![/math]@logistic_guy
Can you please explain?