You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
solving an equation with integrals
- Thread starter Perdurat
- Start date
- Joined
- Nov 24, 2012
- Messages
- 3,021
I would divide through by the constant, and give the definite integrals differentials as follows:
[MATH]\int_{\frac{5}{16}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX[/MATH]
Next, I would look at the indefinite integral:
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du[/MATH]
At this point, I would consider a partial fraction decomposition on the integrand. Can you proceed?
[MATH]\int_{\frac{5}{16}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX[/MATH]
Next, I would look at the indefinite integral:
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du[/MATH]
At this point, I would consider a partial fraction decomposition on the integrand. Can you proceed?
I am afraid I cannot (lack of integral skills)
more over, I am afraid the question doesn't provide the answer i was looking for
allow me to elaborate:
f(x)=[MATH]\frac{6}{(8*X+1)(8*X+4)}[/MATH]the plot comprises 3 parabola, their mirror lines:
Y=AX+B:
for -1/2 > X < -1/8 a1=0, b1=-5/16
for -[MATH]\infty[/MATH] >X< -1/2 a2=a, b2=b
for -1/8 > X < +[MATH]\infty[/MATH] a3=1/a, b3=b
a=?, b=?
more over, I am afraid the question doesn't provide the answer i was looking for
allow me to elaborate:
f(x)=[MATH]\frac{6}{(8*X+1)(8*X+4)}[/MATH]the plot comprises 3 parabola, their mirror lines:
Y=AX+B:
for -1/2 > X < -1/8 a1=0, b1=-5/16
for -[MATH]\infty[/MATH] >X< -1/2 a2=a, b2=b
for -1/8 > X < +[MATH]\infty[/MATH] a3=1/a, b3=b
a=?, b=?
- Joined
- Nov 24, 2012
- Messages
- 3,021
Here is a plot of the integrand:
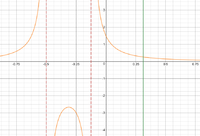
The two vertical asymptotes at [MATH]x=-\frac{1}{2},\,x=-\frac{1}{8}[/MATH] are shown as red dashed lines, and the vertical green line is at [MATH]x=\frac{5}{16}[/MATH].
We are to divide the area under the integrand to the right of this green line into two equal areas, by finding the value of \(x\) where this occurs. I think in order to do that, we need to evaluate both given definite integrals as functions of \(x\), and then solve for \(x\).

The two vertical asymptotes at [MATH]x=-\frac{1}{2},\,x=-\frac{1}{8}[/MATH] are shown as red dashed lines, and the vertical green line is at [MATH]x=\frac{5}{16}[/MATH].
We are to divide the area under the integrand to the right of this green line into two equal areas, by finding the value of \(x\) where this occurs. I think in order to do that, we need to evaluate both given definite integrals as functions of \(x\), and then solve for \(x\).
- Joined
- Nov 24, 2012
- Messages
- 3,021
Using partial fractions, I find:
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du=\frac{1}{6}\ln\left(\frac{8u+1}{2u+1}\right)+C[/MATH]
And so:
[MATH]\int_{\frac{5}{16}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\frac{1}{6}\ln\left(\frac{13(8x+1)}{28(2x+1)}\right)[/MATH]
[MATH]\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX=\frac{1}{6}\ln\left(\frac{4(2x+1)}{8x+1}\right)[/MATH]
This then implies:
[MATH]\frac{13(8x+1)}{28(2x+1)}=\frac{4(2x+1)}{8x+1}[/MATH]
Discarding the negative root, we then find:
[MATH]x=\frac{5+\sqrt{91}}{16}[/MATH]
Using this value, consider the following diagram:
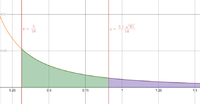
If my calculations are correct (which I fully expect you will verify), then the area shaded in green will be equal to the area shaded in purple (which extends infinitely to the right).
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du=\frac{1}{6}\ln\left(\frac{8u+1}{2u+1}\right)+C[/MATH]
And so:
[MATH]\int_{\frac{5}{16}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\frac{1}{6}\ln\left(\frac{13(8x+1)}{28(2x+1)}\right)[/MATH]
[MATH]\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX=\frac{1}{6}\ln\left(\frac{4(2x+1)}{8x+1}\right)[/MATH]
This then implies:
[MATH]\frac{13(8x+1)}{28(2x+1)}=\frac{4(2x+1)}{8x+1}[/MATH]
Discarding the negative root, we then find:
[MATH]x=\frac{5+\sqrt{91}}{16}[/MATH]
Using this value, consider the following diagram:

If my calculations are correct (which I fully expect you will verify), then the area shaded in green will be equal to the area shaded in purple (which extends infinitely to the right).
thanks for your reply, you're faster than i can prepare answer 
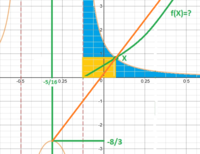
in the original question, i made a typo: should have been -1/8 for the lower bound of the integral in stead of 5/16. I was looking for the symmetry line (eyeballed in red colour), i figured it must be a straight line.... so i figured that the two surfaces coloured in blue must be equal (i totally forgot about the yellow rectangle)
stupid me....
if the symmetry line is indeed a straight line then:
f(x)=ax+b
(-5/8,-8/3) yields -8/3=a*(-5/8)+b
(0,0) yields 0=b
therefore a=64/15
the x,y coordinate of the crossing of f(x)=64/15*x and f(x)=6/(8*x+1)/(8*x+4):
to be continued...

in the original question, i made a typo: should have been -1/8 for the lower bound of the integral in stead of 5/16. I was looking for the symmetry line (eyeballed in red colour), i figured it must be a straight line.... so i figured that the two surfaces coloured in blue must be equal (i totally forgot about the yellow rectangle)
stupid me....
if the symmetry line is indeed a straight line then:
f(x)=ax+b
(-5/8,-8/3) yields -8/3=a*(-5/8)+b
(0,0) yields 0=b
therefore a=64/15
the x,y coordinate of the crossing of f(x)=64/15*x and f(x)=6/(8*x+1)/(8*x+4):
to be continued...
- Joined
- Nov 24, 2012
- Messages
- 3,021
I must admit, I have no idea what you're doing with the "symmetry lines," but if I understand correctly, the actual equation you're trying to solve is:
[MATH]\int_{-\frac{1}{8}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX[/MATH]
We have improper integrals on both sides of the integral. Let's treat these just a bit more formally than I did before. Let's begin with the integral on the LHS of the equation:
[MATH]I_1=\lim_{t\to-\frac{1}{8}}\left(\int_{t}^x\frac{1}{(8X+1)(2X+1)}\,dX\right)[/MATH]
Using the anti-derivative I previously posted, that is:
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du=\frac{1}{6}\ln\left(\frac{8u+1}{2u+1}\right)+C[/MATH]
We may then state:
[MATH]I_1=\frac{1}{6}\lim_{t\to-\frac{1}{8}}\left(\ln\left(\frac{(8x+1)(2t+1)}{(2x+1)(8t+1)}\right)\right)[/MATH]
Alas, we find this integral does not converge. We know the integral on the RHS does converge, and so we I would say we cannot solve the equation.
[MATH]\int_{-\frac{1}{8}}^x\frac{1}{(8X+1)(2X+1)}\,dX=\int_{x}^{\infty}\frac{1}{(8X+1)(2X+1)}\,dX[/MATH]
We have improper integrals on both sides of the integral. Let's treat these just a bit more formally than I did before. Let's begin with the integral on the LHS of the equation:
[MATH]I_1=\lim_{t\to-\frac{1}{8}}\left(\int_{t}^x\frac{1}{(8X+1)(2X+1)}\,dX\right)[/MATH]
Using the anti-derivative I previously posted, that is:
[MATH]\int \frac{1}{(8u+1)(2u+1)}\,du=\frac{1}{6}\ln\left(\frac{8u+1}{2u+1}\right)+C[/MATH]
We may then state:
[MATH]I_1=\frac{1}{6}\lim_{t\to-\frac{1}{8}}\left(\ln\left(\frac{(8x+1)(2t+1)}{(2x+1)(8t+1)}\right)\right)[/MATH]
Alas, we find this integral does not converge. We know the integral on the RHS does converge, and so we I would say we cannot solve the equation.
thanks for reply,
meanwhile i "resolved some of my idiot braincells"
consider:
[MATH]\pi =\sum _{n=0}^{\infty }\:\frac{1}{^{16^n}}\left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right)[/MATH] (Simon Plouffe, spigot algorythm)
changing a bit the format:
[MATH]\pi =\sum _{n=0}^{\infty }\:\frac{1}{16^n}\left(2\alpha +\beta +\gamma \right)[/MATH][MATH]\alpha =\frac{3}{\left(8n+1\right)\left(8n+4\right)}[/MATH][MATH]\beta =\frac{4}{\left(8n+1\right)\left(8n+5\right)}[/MATH][MATH]\gamma =\frac{5}{\left(8n+1\right)\left(8n+6\right)}[/MATH]solving those equations, yields the digits of pi in hexadecimal format
so 3 functions (a smooth slope,except for 4 values of x) + a hexadecimal number system (16^0,16^-1,16^-2,...)=erratic number sequence (pi)
so what is special about 16 ? the only thing i can think of : 16 = 2^4 = 4^2 (far as i know, that is a unique property)
so what is special about those functions? ([MATH]\alpha,\beta,\gamma)[/MATH][MATH]2\alpha[/MATH] in original post)
general format: [MATH]f(x)=ax^2+bx+c[/MATH] (red curve, dark blue symmetry line)
plugged into: [MATH]f(x)=\frac{1}{x}[/MATH] (light blue curve, green symmetry line)
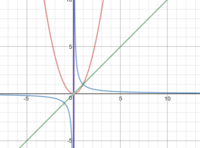
(correct me if i am wrong)
so for those general functions:
[MATH]f\left(x\right)=ax^2\rightarrow \:\int _{-\infty }^0\:x^2dx\:=\:\int _0^{+\infty }\:x^2dx[/MATH]this should yield x=0
[MATH]f\left(x\right)=\frac{1}{x}\rightarrow \:\int _0^x\:\frac{1}{x}dx-x\cdot \frac{1}{x}=\int _x^{-\infty }\:\frac{1}{x}dx[/MATH]this should yield x=1
in laymen's terms:
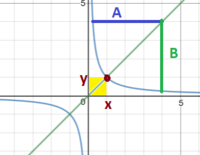
when a point (x,y) is moved on the symmetry line towards infinity, A remains equal to B
moving back to one of these functions, slightly modified:
[MATH]\alpha \:=\frac{3}{\left(8\left(x-\frac{1}{8}\right)+1\right)\left(8\left(x-\frac{1}{8}\right)+4\right)}[/MATH][MATH]\alpha\:=\frac{3}{8x\left(8x+3\right)}[/MATH][MATH]\beta\:=\frac{4}{8x\left(8x+4\right)}[/MATH][MATH]\gamma\:=\frac{5}{8x\left(8x+5\right)}[/MATH]now that the curve ([MATH]\alpha[/MATH]) is moved an amount to the right, the quadrant (+X+,+Y) is the one i am interested in. the quest remains: how to find the function for the curve (symmetry curve, so to speak), such that A remains equal to B ?
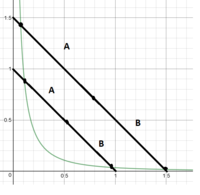
the point where x=y intersects with [MATH]\alpha\:=\frac{3}{8x\left(8x+3\right)}[/MATH](x must be >0)
[MATH]x\:=\frac{3}{8x\left(8x+3\right)}[/MATH]so how to resolve? (finding a definition for that partial function(from x derived from above to limit of indefinite)
meanwhile i "resolved some of my idiot braincells"
consider:
[MATH]\pi =\sum _{n=0}^{\infty }\:\frac{1}{^{16^n}}\left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right)[/MATH] (Simon Plouffe, spigot algorythm)
changing a bit the format:
[MATH]\pi =\sum _{n=0}^{\infty }\:\frac{1}{16^n}\left(2\alpha +\beta +\gamma \right)[/MATH][MATH]\alpha =\frac{3}{\left(8n+1\right)\left(8n+4\right)}[/MATH][MATH]\beta =\frac{4}{\left(8n+1\right)\left(8n+5\right)}[/MATH][MATH]\gamma =\frac{5}{\left(8n+1\right)\left(8n+6\right)}[/MATH]solving those equations, yields the digits of pi in hexadecimal format
so 3 functions (a smooth slope,except for 4 values of x) + a hexadecimal number system (16^0,16^-1,16^-2,...)=erratic number sequence (pi)
so what is special about 16 ? the only thing i can think of : 16 = 2^4 = 4^2 (far as i know, that is a unique property)
so what is special about those functions? ([MATH]\alpha,\beta,\gamma)[/MATH][MATH]2\alpha[/MATH] in original post)
general format: [MATH]f(x)=ax^2+bx+c[/MATH] (red curve, dark blue symmetry line)
plugged into: [MATH]f(x)=\frac{1}{x}[/MATH] (light blue curve, green symmetry line)

(correct me if i am wrong)
so for those general functions:
[MATH]f\left(x\right)=ax^2\rightarrow \:\int _{-\infty }^0\:x^2dx\:=\:\int _0^{+\infty }\:x^2dx[/MATH]this should yield x=0
[MATH]f\left(x\right)=\frac{1}{x}\rightarrow \:\int _0^x\:\frac{1}{x}dx-x\cdot \frac{1}{x}=\int _x^{-\infty }\:\frac{1}{x}dx[/MATH]this should yield x=1
in laymen's terms:

when a point (x,y) is moved on the symmetry line towards infinity, A remains equal to B
moving back to one of these functions, slightly modified:
[MATH]\alpha \:=\frac{3}{\left(8\left(x-\frac{1}{8}\right)+1\right)\left(8\left(x-\frac{1}{8}\right)+4\right)}[/MATH][MATH]\alpha\:=\frac{3}{8x\left(8x+3\right)}[/MATH][MATH]\beta\:=\frac{4}{8x\left(8x+4\right)}[/MATH][MATH]\gamma\:=\frac{5}{8x\left(8x+5\right)}[/MATH]now that the curve ([MATH]\alpha[/MATH]) is moved an amount to the right, the quadrant (+X+,+Y) is the one i am interested in. the quest remains: how to find the function for the curve (symmetry curve, so to speak), such that A remains equal to B ?

the point where x=y intersects with [MATH]\alpha\:=\frac{3}{8x\left(8x+3\right)}[/MATH](x must be >0)
[MATH]x\:=\frac{3}{8x\left(8x+3\right)}[/MATH]so how to resolve? (finding a definition for that partial function(from x derived from above to limit of indefinite)
